Recently, I was asked to generate a list of all cities that would be impacted by one of our marketing initiatives, and I figured… « Hey but that could be useful for our geo-targeted emails, facebook marketing campaigns… any location based investements or initiative that either require a zip code or a city name ».

Targeting a publication on Facebook is definitely not the nigthmare it used to be but when you are looking for a granular list of all cities around your geo-targeted city… the nightmare comes back… You have to type in every city you want to specifically target, there are no radius or maping as with Google AdWords :

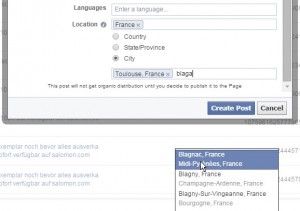
And usually it is roughly the same thing with emailing: you can’t just input a location, you have to use the customer’s zip code to properly target him/her in your emailing campaign.

So what does that excel spreadsheet do?

It helps you filter any location database (where you have latitude and longitude): this helps you filter any city/zip code within certain constraints, outputing the zip-code of every cities you want to target, (edit oct-29th) and giving you a rough estimate of the population of your targeted area (see biggest cities method).
I built two methods :

1. The rectangle Method
2. The Radius Method
3. edit oct-29th: The biggest cities method

The rectangle Method

As its name clearly says this will help you determine from 4 GPS coordinates what cities/zip code you want to target.
Just head to Google Maps (or wherever you can spot Decimal degrees coordinates), and spot the 4 angles of your rectangle (right click and « what here », you’ll have a tooltip at the bottom of the map with the decimal GPS coordinates)

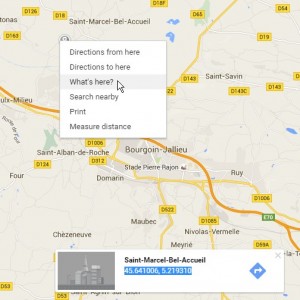
Spot the 4 angles of your rectangle and input them in cells N4:O7

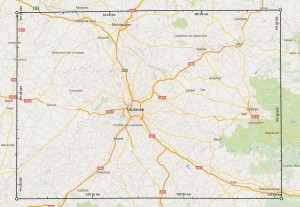
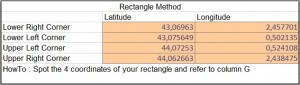
And basically you are done !
Column I (« Proximity (Rectangle) ») will tell you if the city is within the largest boundaries of your rectangle : « In » or « Out »

How does it work?

That’s fairly straightforward, let’s have a look at the formula (in cell I2):

=IF(AND(AND(E2>MIN($N$4:$N$7);E2<MAX($N$4:$N$7));AND(F2>MIN($O$4:$O$7);F2<MAX($O$4:$O$7))); »in »; »out »)

We just have to compare the latitude of each city an:

• ensure it’s higher than the minimum of the rectangle’s lat
• and lower than the maximum lat of the rectangle
• same for long
• If that’s the case it’s « In »; if not it’s « out »

Well that does the job… but was not satisfactory in my opinion. I wanted a radius. So here is the second method:

The Radius Method

Well I’m not being completely honest here… I didn’t find what I was really looking for but I found a cool enough work around:
As we have all GPS coodinates of each city, we can actually compute the distance of that city to a given GPS point.
So back to Google Maps, get the GPS coordinate of the center your radius, and input it in cells N13:14.
Then pick the radius you want in kilometers (ex: 90)… and you’re done !

Column J gives the distance between each city and the GPS coordinates you entered and column K (I decomposed on purpuse) will check if that distance is below the radius you picked in cell N15.

How does that one work ?

I had to get some help for that one… and found Chip Pearson’s blog post on GPS coordinates and calculations.
I’ll let you read… but it uses the method of Great Circle Distances and I quote:

Great Circle Distances

In Mathematics and Cartography, a Great Circle Distance is the shortest path between two points on the surface of a sphere (and we will assume that the Earth is a perfect sphere, even though it really isn’t). This is the « as the crow files » distance between the two points. All lines of Longitude are Great Circles, while the Equator is the only Latitudinal Great Circle.

To calculate the Great Circle Distance between points, we first calculate the spherical central angle between the two points and then multiply that angle (in Radians) by the radius of the Earth.

So here is the fomula in cell J2:

=6370,97327862273*((2*ASIN(SQRT((SIN((RADIANS(E2)-RADIANS($N$13))/2)^2)+COS(RADIANS(E2))*COS(RADIANS($N$13))*(SIN((RADIANS(F2)-RADIANS($N$14))/2)^2)))))

6370,97327862273 is the earth radius in km assuming it’s a perfect sphere as Chip said.

So here you are: you have the distance to your given location… and just have to know whether or not it’s under your radius or not.

The Biggest cities Method

Paragraph added oct-29th:
I wasn’t fully happy when I had finished designing the first version of my spreadsheet… I wanted to find out the targeted population once you had input the radius or defined the target area… so I went back to the web and found a new, more comprehensive database with the population of each city. So, now… thanks to a nice « countIf » and a sumif we can output the population the area targeted by any method and the number of cities targeted as well… and VOILA you have a new header:

Anyway… now that we have a DB with all cities… and their population, it’s fairly easy to create a filter with only the biggest cities in France… because your targeting is often going to be around these cities, making the file easier to use!

The concept is exactly the same as the radius method and the formulas are the same, I just added a dropdown list with all major cities, from which I fetch the GPS coordinates from a separte DB (I could have used the same one but for lisibility I prefered using a different tab and table) (If you have a nice idea on how to create a variable dropdown list from a database, let me know 🙂

So just select a city… and BOOM done!

Sweet right? Thoughts? Any idea on how to map it now?

Sources:

For the french database I found that almost complete database (missing 1321 cities in France): http://blog.chto.fr/2013/02/divers-villes-codes-postaux-coordonnees-gps-et-departement/
As I was telling on the 3rd method, I found a more comprehensive DB: http://sql.sh/736-base-donnees-villes-francaises
and for my US friends you can find one here: http://www.boutell.com/zipcodes/
Last, this link suggested by CheeseCode.fr which gave me the radius idea.

Files

you can download the first version of the sample file here

Edit: here is the second version (a bit heavier… 10Mb)